Algebra zu lernen kann einschüchternd wirken, aber wenn man einmal den Dreh raus hat, ist es gar nicht so schwer! Sie müssen nur der Reihenfolge folgen, um Teile der Gleichung zu vervollständigen und Ihre Arbeit organisiert zu halten, um Fehler zu vermeiden!
Teil eins von fünf:
Grundlegende Algebra-Regeln lernen
-
 1 Überprüfen Sie Ihre grundlegenden mathematischen Operationen. Um Algebra zu lernen, müssen Sie grundlegende mathematische Fähigkeiten wie Addieren, Subtrahieren, Multiplizieren und Dividieren kennen. Diese Grund- / Grundschulmathematik ist wichtig, bevor Sie anfangen, Algebra zu lernen. Wenn Sie diese Fähigkeiten nicht beherrschen, wird es schwierig, die komplexeren Konzepte der Algebra zu bewältigen. Wenn Sie diese Operationen auffrischen möchten, lesen Sie unseren Artikel über grundlegende mathematische Fähigkeiten.
1 Überprüfen Sie Ihre grundlegenden mathematischen Operationen. Um Algebra zu lernen, müssen Sie grundlegende mathematische Fähigkeiten wie Addieren, Subtrahieren, Multiplizieren und Dividieren kennen. Diese Grund- / Grundschulmathematik ist wichtig, bevor Sie anfangen, Algebra zu lernen. Wenn Sie diese Fähigkeiten nicht beherrschen, wird es schwierig, die komplexeren Konzepte der Algebra zu bewältigen. Wenn Sie diese Operationen auffrischen möchten, lesen Sie unseren Artikel über grundlegende mathematische Fähigkeiten. - Du musst nicht unbedingt sein groß bei diesen grundlegenden Operationen in deinem Kopf Algebra Probleme zu tun. Viele Algebra-Klassen ermöglichen es Ihnen, einen Taschenrechner zu verwenden, um Zeit zu sparen, wenn Sie diese einfachen Operationen ausführen. Sie sollten jedoch zumindest wissen, wie Sie diese Operationen ohne einen Rechner durchführen, wenn Sie keinen verwenden dürfen.
-
 2 Kennen Sie die Reihenfolge der Vorgänge. Eines der schwierigsten Dinge beim Lösen einer Algebra-Gleichung als Anfänger ist zu wissen, wo ich anfangen soll. Glücklicherweise gibt es eine bestimmte Reihenfolge, um diese Probleme zu lösen: machen Sie zuerst alle mathematischen Operationen in Klammern, dann tun Sie Exponenten, dann multiplizieren Sie, dann teilen Sie, fügen Sie dann hinzu, und subtrahieren Sie schließlich. Ein praktisches Werkzeug zur Erinnerung an diese Reihenfolge von Operationen ist das Akronym PEMDAS. Hier erfahren Sie, wie Sie die Reihenfolge der Operationen anwenden. Zur Erinnerung, die Reihenfolge der Operationen ist:
2 Kennen Sie die Reihenfolge der Vorgänge. Eines der schwierigsten Dinge beim Lösen einer Algebra-Gleichung als Anfänger ist zu wissen, wo ich anfangen soll. Glücklicherweise gibt es eine bestimmte Reihenfolge, um diese Probleme zu lösen: machen Sie zuerst alle mathematischen Operationen in Klammern, dann tun Sie Exponenten, dann multiplizieren Sie, dann teilen Sie, fügen Sie dann hinzu, und subtrahieren Sie schließlich. Ein praktisches Werkzeug zur Erinnerung an diese Reihenfolge von Operationen ist das Akronym PEMDAS. Hier erfahren Sie, wie Sie die Reihenfolge der Operationen anwenden. Zur Erinnerung, die Reihenfolge der Operationen ist: - PKlammern
- EKomponenten
- MEndgültigkeit
- Division
- EINdition
- SSubtraktion
- Die Reihenfolge der Operationen ist in der Algebra wichtig, da die Ausführung der Operationen in einem Algebra-Problem in der falschen Reihenfolge manchmal die Antwort beeinflussen kann. Zum Beispiel, wenn wir uns mit dem mathematischen Problem 8 + 2 × 5 befassen, wenn wir zuerst 2 bis 8 addieren, erhalten wir 10 × 5 = 50, aber wenn wir zuerst 2 und 5 multiplizieren, erhalten wir 8 + 10 = 18. Nur die zweite Antwort ist richtig.
-
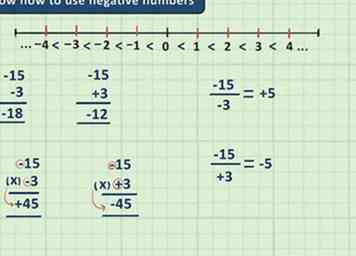 3 Wissen, wie man negative Zahlen benutzt. In der Algebra ist es üblich, negative Zahlen zu verwenden. Daher ist es ratsam zu überprüfen, wie man Negative addiert, subtrahiert, multipliziert und teilt, bevor man mit Algebra beginnt. Im Folgenden sind nur ein paar Zahlen zu negativen Zahlen zu beachten. Weitere Informationen finden Sie in unseren Artikeln zum Hinzufügen und Subtrahieren negativer Zahlen und zum Dividieren und Multiplizieren negativer Zahlen.
3 Wissen, wie man negative Zahlen benutzt. In der Algebra ist es üblich, negative Zahlen zu verwenden. Daher ist es ratsam zu überprüfen, wie man Negative addiert, subtrahiert, multipliziert und teilt, bevor man mit Algebra beginnt. Im Folgenden sind nur ein paar Zahlen zu negativen Zahlen zu beachten. Weitere Informationen finden Sie in unseren Artikeln zum Hinzufügen und Subtrahieren negativer Zahlen und zum Dividieren und Multiplizieren negativer Zahlen. - In einer Zahlenzeile ist eine negative Version einer Zahl die gleiche Entfernung von Null wie die positive, aber in der entgegengesetzten Richtung.
- Das Hinzufügen von zwei negativen Zahlen ergibt die Nummer negativer (Mit anderen Worten, die Ziffern sind höher, aber da die Zahl negativ ist, zählt sie als niedriger)
- Zwei negative Zeichen heben sich auf - das Subtrahieren einer negativen Zahl ist das Gleiche wie das Hinzufügen einer positiven Zahl
- Die Multiplikation oder Division zweier negativer Zahlen ergibt eine positive Antwort.
- Das Multiplizieren oder Dividieren einer positiven Zahl und einer negativen Zahl ergibt eine negative Antwort.
-
 4 Wissen, wie man lange Probleme organisiert. Während einfache Algebra-Probleme ein Kinderspiel sein können, können kompliziertere Probleme viele, viele Schritte erfordern. Um Fehler zu vermeiden, sollten Sie Ihre Arbeit organisieren, indem Sie jedes Mal eine neue Zeile beginnen, wenn Sie einen Schritt zur Lösung Ihres Problems machen. Wenn Sie mit einer zweiseitigen Gleichung arbeiten, versuchen Sie, alle Gleichheitszeichen ("=" s) untereinander zu schreiben. Auf diese Weise, wenn Sie irgendwo einen Fehler machen, wird es viel einfacher zu finden und zu korrigieren.
4 Wissen, wie man lange Probleme organisiert. Während einfache Algebra-Probleme ein Kinderspiel sein können, können kompliziertere Probleme viele, viele Schritte erfordern. Um Fehler zu vermeiden, sollten Sie Ihre Arbeit organisieren, indem Sie jedes Mal eine neue Zeile beginnen, wenn Sie einen Schritt zur Lösung Ihres Problems machen. Wenn Sie mit einer zweiseitigen Gleichung arbeiten, versuchen Sie, alle Gleichheitszeichen ("=" s) untereinander zu schreiben. Auf diese Weise, wenn Sie irgendwo einen Fehler machen, wird es viel einfacher zu finden und zu korrigieren. - Um zum Beispiel die Gleichung 9/3 - 5 + 3 × 4 zu lösen, könnten wir unser Problem so organisieren:
-
- 9/3 - 5 + 3 × 4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- 10
-
- Um zum Beispiel die Gleichung 9/3 - 5 + 3 × 4 zu lösen, könnten wir unser Problem so organisieren:
Teil Zwei von Fünf:
Variablen verstehen
-
 1 Suchen Sie nach Symbolen, die keine Zahlen sind. In der Algebra werden Sie anfangen, Buchstaben und Symbole in Ihren mathematischen Problemen zu sehen, und nicht nur Zahlen. Dies nennt man Variablen. Variablen sind nicht so verwirrend, wie sie zuerst erscheinen - sie sind nur Möglichkeiten, Zahlen mit unbekannten Werten zu zeigen. Im Folgenden finden Sie nur einige häufige Beispiele für Variablen in der Algebra:
1 Suchen Sie nach Symbolen, die keine Zahlen sind. In der Algebra werden Sie anfangen, Buchstaben und Symbole in Ihren mathematischen Problemen zu sehen, und nicht nur Zahlen. Dies nennt man Variablen. Variablen sind nicht so verwirrend, wie sie zuerst erscheinen - sie sind nur Möglichkeiten, Zahlen mit unbekannten Werten zu zeigen. Im Folgenden finden Sie nur einige häufige Beispiele für Variablen in der Algebra: - Buchstaben wie x, y, z, a, b und c
- Griechische Buchstaben wie Theta oder θ
- Beachten Sie, dass nicht alle Symbole sind unbekannte Variablen. Zum Beispiel ist pi oder π immer gleich ungefähr 3,14159.
-
 2 Stellen Sie sich Variablen als "unbekannte" Zahlen vor. Wie oben erwähnt, sind Variablen im Grunde nur Zahlen mit unbekannten Werten. Mit anderen Worten, da ist eine Nummer das kann anstelle der Variablen gehen, damit die Gleichung funktioniert. Normalerweise ist Ihr Ziel in einem Algebra-Problem, herauszufinden, was die Variable ist - denken Sie an sie als eine "Mystery-Nummer", die Sie zu entdecken versuchen.
2 Stellen Sie sich Variablen als "unbekannte" Zahlen vor. Wie oben erwähnt, sind Variablen im Grunde nur Zahlen mit unbekannten Werten. Mit anderen Worten, da ist eine Nummer das kann anstelle der Variablen gehen, damit die Gleichung funktioniert. Normalerweise ist Ihr Ziel in einem Algebra-Problem, herauszufinden, was die Variable ist - denken Sie an sie als eine "Mystery-Nummer", die Sie zu entdecken versuchen. - Zum Beispiel ist in der Gleichung 2x + 3 = 11 x unsere Variable. Das bedeutet, dass an der Stelle von x ein Wert steht, der die linke Seite der Gleichung gleich 11 macht. Da 2 × 4 + 3 = 11, in diesem Fall x = 4.
- Eine einfache Möglichkeit, Variablen zu verstehen, besteht darin, sie durch Fragezeichen in Algebra-Problemen zu ersetzen. Zum Beispiel könnten wir die Gleichung 2 + 3 + x = 9 als 2 + 3 + neu schreiben ? = 9. Dies macht es einfacher zu verstehen, was wir versuchen zu tun - wir müssen nur herausfinden, welche Nummer zu 2 + 3 = 5 hinzufügen, um 9 zu bekommen. Die Antwort ist wieder 4, Na sicher.
-
 3 Achten Sie auf wiederkehrende Variablen. Wenn eine Variable mehr als einmal auftritt, vereinfachen Sie die Variablen. Was tun Sie, wenn die gleiche Variable mehr als einmal in der Gleichung erscheint? Obwohl diese Situation schwierig zu lösen scheint, können Sie Variablen tatsächlich behandeln, wie Sie normale Zahlen behandeln würden - mit anderen Worten, Sie können sie hinzufügen, subtrahieren und so weiter, solange Sie nur identische Variablen kombinieren. Mit anderen Worten, x + x = 2x, aber x + y ist nicht gleich 2xy.
3 Achten Sie auf wiederkehrende Variablen. Wenn eine Variable mehr als einmal auftritt, vereinfachen Sie die Variablen. Was tun Sie, wenn die gleiche Variable mehr als einmal in der Gleichung erscheint? Obwohl diese Situation schwierig zu lösen scheint, können Sie Variablen tatsächlich behandeln, wie Sie normale Zahlen behandeln würden - mit anderen Worten, Sie können sie hinzufügen, subtrahieren und so weiter, solange Sie nur identische Variablen kombinieren. Mit anderen Worten, x + x = 2x, aber x + y ist nicht gleich 2xy. - Betrachten wir zum Beispiel die Gleichung 2x + 1x = 9. In diesem Fall können wir 2x und 1x addieren, um 3x = 9 zu erhalten. Da 3 x 3 = 9, wissen wir, dass x = 3.
- Beachten Sie erneut, dass Sie nur die gleichen Variablen hinzufügen können. In der Gleichung 2x + 1y = 9 können wir 2x und 1y nicht kombinieren, weil sie zwei verschiedene Variablen sind.
- Dies gilt auch, wenn eine Variable einen anderen Exponenten hat als ein anderer. Zum Beispiel in der Gleichung 2x + 3x2 = 10, wir können nicht 2x und 3x kombinieren2 weil die x-Variablen unterschiedliche Exponenten haben. Weitere Informationen finden Sie unter Hinzufügen von Exponenten.
Teil Drei von Fünf:
Gleichungen durch "Annullieren" lösen lernen
-
 1 Versuchen Sie, die Variable selbst in Algebra-Gleichungen zu erhalten. Das Lösen einer Gleichung in der Algebra bedeutet normalerweise, herauszufinden, was die Variable ist. Algebra-Gleichungen werden normalerweise mit Zahlen und / oder Variablen auf beiden Seiten erstellt, wie folgt: x + 2 = 9 × 4. Um herauszufinden, was die Variable ist, müssen Sie sie selbst auf einer Seite des Gleichheitszeichens erhalten. Was immer auf der anderen Seite des Gleichheitszeichens ist, ist deine Antwort.
1 Versuchen Sie, die Variable selbst in Algebra-Gleichungen zu erhalten. Das Lösen einer Gleichung in der Algebra bedeutet normalerweise, herauszufinden, was die Variable ist. Algebra-Gleichungen werden normalerweise mit Zahlen und / oder Variablen auf beiden Seiten erstellt, wie folgt: x + 2 = 9 × 4. Um herauszufinden, was die Variable ist, müssen Sie sie selbst auf einer Seite des Gleichheitszeichens erhalten. Was immer auf der anderen Seite des Gleichheitszeichens ist, ist deine Antwort. - Im Beispiel (x + 2 = 9 × 4) müssen wir, um x auf der linken Seite der Gleichung zu erhalten, das "+ 2" loswerden. Um dies zu tun, subtrahieren wir einfach 2 von dieser Seite und lassen uns mit x = 9 × 4. Um jedoch beide Seiten der Gleichung gleich zu halten, müssen wir auch 2 von der anderen Seite subtrahieren. Dies lässt uns mit x = 9 × 4 - 2. Nach der Reihenfolge der Operationen, multiplizieren wir zuerst, dann subtrahieren, geben uns eine Antwort von x = 36 - 2 = 34.
-
 2 Addition mit Subtraktion abbrechen (und umgekehrt). Wie wir gerade oben gesehen haben, bedeutet es, wenn man x auf einer Seite des Gleichheitszeichens erhält, normalerweise die Zahlen daneben loszuwerden. Um dies zu tun, führen wir die "entgegengesetzte" Operation auf beiden Seiten der Gleichung durch. Zum Beispiel, in der Gleichung x + 3 = 0, da wir ein "+ 3" neben unserem x sehen, setzen wir eine "- 3" auf beide Seiten. Die "+ 3" und "- 3", x auf sich selbst und "-3" auf der anderen Seite des Gleichheitszeichens, wie folgt: x = -3.
2 Addition mit Subtraktion abbrechen (und umgekehrt). Wie wir gerade oben gesehen haben, bedeutet es, wenn man x auf einer Seite des Gleichheitszeichens erhält, normalerweise die Zahlen daneben loszuwerden. Um dies zu tun, führen wir die "entgegengesetzte" Operation auf beiden Seiten der Gleichung durch. Zum Beispiel, in der Gleichung x + 3 = 0, da wir ein "+ 3" neben unserem x sehen, setzen wir eine "- 3" auf beide Seiten. Die "+ 3" und "- 3", x auf sich selbst und "-3" auf der anderen Seite des Gleichheitszeichens, wie folgt: x = -3. - Im Allgemeinen sind Addition und Subtraktion wie "Gegensätze" - machen Sie einen, um den anderen loszuwerden. Siehe unten:
-
- Für die Addition subtrahieren. Beispiel: x + 9 = 3 → x = 3 - 9
- Für die Subtraktion hinzufügen. Beispiel: x - 4 = 20 → x = 20 + 4
-
- Im Allgemeinen sind Addition und Subtraktion wie "Gegensätze" - machen Sie einen, um den anderen loszuwerden. Siehe unten:
-
 3 Multiplikation mit Division abbrechen (und umgekehrt). Multiplikation und Division sind etwas schwieriger zu bearbeiten als Addition und Subtraktion, aber sie haben die gleiche "umgekehrte" Beziehung. Wenn Sie auf einer Seite ein "× 3" sehen, werden Sie es abbrechen, indem Sie beide Seiten durch 3 teilen, und so weiter.
3 Multiplikation mit Division abbrechen (und umgekehrt). Multiplikation und Division sind etwas schwieriger zu bearbeiten als Addition und Subtraktion, aber sie haben die gleiche "umgekehrte" Beziehung. Wenn Sie auf einer Seite ein "× 3" sehen, werden Sie es abbrechen, indem Sie beide Seiten durch 3 teilen, und so weiter. - Bei Multiplikation und Division müssen Sie die umgekehrte Operation ausführen alles auf der anderen Seite des Gleichheitszeichens, auch wenn es mehr als eine Zahl ist. Siehe unten:
-
- Multiplikation, dividieren. Beispiel: 6x = 14 + 2 → x = (14 + 2)/6
- Für die Division multiplizieren. Beispiel: x / 5 = 25 → x = 25 × 5
-
- Bei Multiplikation und Division müssen Sie die umgekehrte Operation ausführen alles auf der anderen Seite des Gleichheitszeichens, auch wenn es mehr als eine Zahl ist. Siehe unten:
-
 4 Brechen Sie Exponenten ab, indem Sie die Wurzel nehmen (und umgekehrt). Exponenten sind ein ziemlich fortgeschrittenes Voralgebra-Thema - wenn Sie nicht wissen, wie Sie es tun, finden Sie in unserem grundlegenden Exponenten Artikel für weitere Informationen. Das "Gegenteil" eines Exponenten ist die Wurzel, die dieselbe Zahl hat wie sie. Zum Beispiel das Gegenteil von der 2 Exponent ist eine Quadratwurzel (√), das Gegenteil von der 3 Exponent ist die Kubikwurzel (3√) und so weiter.
4 Brechen Sie Exponenten ab, indem Sie die Wurzel nehmen (und umgekehrt). Exponenten sind ein ziemlich fortgeschrittenes Voralgebra-Thema - wenn Sie nicht wissen, wie Sie es tun, finden Sie in unserem grundlegenden Exponenten Artikel für weitere Informationen. Das "Gegenteil" eines Exponenten ist die Wurzel, die dieselbe Zahl hat wie sie. Zum Beispiel das Gegenteil von der 2 Exponent ist eine Quadratwurzel (√), das Gegenteil von der 3 Exponent ist die Kubikwurzel (3√) und so weiter. - Es mag ein wenig verwirrend sein, aber in diesen Fällen nehmen Sie die Wurzel beider Seiten, wenn Sie mit einem Exponenten zu tun haben. Auf der anderen Seite nehmen Sie den Exponenten beider Seiten, wenn Sie mit einer Wurzel zu tun haben. Siehe unten:
-
- Für Exponenten, nehmen Sie die Wurzel. Beispiel: x2 = 49 → x = √49
- Für Wurzeln nehmen Sie den Exponenten. Beispiel: √x = 12 → x = 122
-
- Es mag ein wenig verwirrend sein, aber in diesen Fällen nehmen Sie die Wurzel beider Seiten, wenn Sie mit einem Exponenten zu tun haben. Auf der anderen Seite nehmen Sie den Exponenten beider Seiten, wenn Sie mit einer Wurzel zu tun haben. Siehe unten:
Teil vier von fünf:
Schärfen Sie Ihre Algebra Skills
-
 1 Verwenden Sie Bilder, um Probleme zu verdeutlichen. Wenn Sie Probleme bei der Visualisierung eines Algebraproblems haben, versuchen Sie es mit Hilfe von Diagrammen oder Bildern, um Ihre Gleichung zu veranschaulichen. Sie können sogar versuchen, eine Gruppe von physischen Objekten (wie Blöcke oder Münzen) zu verwenden, wenn Sie etwas handliches haben.
1 Verwenden Sie Bilder, um Probleme zu verdeutlichen. Wenn Sie Probleme bei der Visualisierung eines Algebraproblems haben, versuchen Sie es mit Hilfe von Diagrammen oder Bildern, um Ihre Gleichung zu veranschaulichen. Sie können sogar versuchen, eine Gruppe von physischen Objekten (wie Blöcke oder Münzen) zu verwenden, wenn Sie etwas handliches haben. - Lassen Sie uns zum Beispiel die Gleichung x + 2 = 3 mithilfe von Kästchen (☐) lösen.
-
- x +2 = 3
- ☒+☐☐ =☐☐☐
- An dieser Stelle ziehen wir 2 von beiden Seiten ab, indem wir einfach 2 Kästchen (☐☐) von beiden Seiten entfernen:
- ☒+☐☐-☐☐ =☐☐☐-☐☐
- ☒ = ☐ oder x = 1
-
- Als ein anderes Beispiel, versuchen wir 2x = 4
-
- ☒☒ =☐☐☐☐
- An diesem Punkt werden wir beide Seiten durch zwei teilen, indem wir die Kästchen auf jeder Seite in zwei Gruppen trennen:
- ☒|☒ =☐☐|☐☐
- ☒ = ☐☐ oder x = 2
-
- Lassen Sie uns zum Beispiel die Gleichung x + 2 = 3 mithilfe von Kästchen (☐) lösen.
-
 2 Verwenden Sie "Common-Sense-Checks" (besonders bei Wortproblemen). Versuchen Sie beim Konvertieren eines Wortproblems in Algebra Ihre Formel zu überprüfen, indem Sie einfache Werte für Ihre Variable einfügen. Ist Ihre Gleichung sinnvoll, wenn x = 0? Wenn x = 1? Wenn x = -1? Es ist leicht, einfache Fehler zu machen, indem du p = 6d aufschreibst, wenn du p = d / 6 meinst, aber diese werden leicht aufgefangen, wenn du eine schnelle Vernunftprüfung an deiner Arbeit durchführst, bevor du weiter gehst.
2 Verwenden Sie "Common-Sense-Checks" (besonders bei Wortproblemen). Versuchen Sie beim Konvertieren eines Wortproblems in Algebra Ihre Formel zu überprüfen, indem Sie einfache Werte für Ihre Variable einfügen. Ist Ihre Gleichung sinnvoll, wenn x = 0? Wenn x = 1? Wenn x = -1? Es ist leicht, einfache Fehler zu machen, indem du p = 6d aufschreibst, wenn du p = d / 6 meinst, aber diese werden leicht aufgefangen, wenn du eine schnelle Vernunftprüfung an deiner Arbeit durchführst, bevor du weiter gehst. - Nehmen wir zum Beispiel an, dass ein Fußballfeld 27,4 Meter länger ist als breit. Wir verwenden die Gleichung l = w + 30, um dies darzustellen. Wir können testen, ob diese Gleichung sinnvoll ist, indem wir einfache Werte für w einfügen. Wenn das Feld beispielsweise w = 10 yards (9,1 m) breit ist, wird es 10 + 30 = 40 yards (36,6 m) lang sein. Wenn es 27,4 m breit ist, wird es 30 + 30 = 60 yards (54,9 m) lang und so weiter. Das ist sinnvoll - wir würden erwarten, dass das Feld länger wird, wenn es breiter wird, also ist diese Gleichung vernünftig.
-
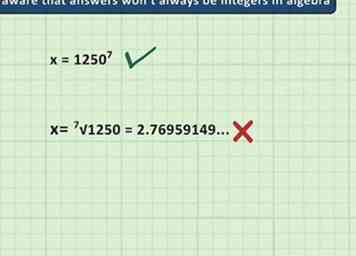 3 Seien Sie sich bewusst, dass die Antworten in der Algebra nicht immer ganzzahlig sind. Die Antworten auf Algebra und andere fortgeschrittene Formen der Mathematik sind nicht immer runde, einfache Zahlen. Sie können oft Dezimalzahlen, Brüche oder irrationale Zahlen sein. Ein Taschenrechner kann Ihnen helfen, diese komplizierten Antworten zu finden, aber denken Sie daran, dass Ihr Lehrer möglicherweise verlangt, dass Sie Ihre Antwort in ihrer genauen Form und nicht in einer unhandlichen Dezimalzahl geben.
3 Seien Sie sich bewusst, dass die Antworten in der Algebra nicht immer ganzzahlig sind. Die Antworten auf Algebra und andere fortgeschrittene Formen der Mathematik sind nicht immer runde, einfache Zahlen. Sie können oft Dezimalzahlen, Brüche oder irrationale Zahlen sein. Ein Taschenrechner kann Ihnen helfen, diese komplizierten Antworten zu finden, aber denken Sie daran, dass Ihr Lehrer möglicherweise verlangt, dass Sie Ihre Antwort in ihrer genauen Form und nicht in einer unhandlichen Dezimalzahl geben. - Nehmen wir zum Beispiel an, dass wir eine Algebragleichung auf x = 1250 eingrenzen7. Wenn wir 1250 eingeben7 In einen Taschenrechner erhalten wir eine riesige Folge von Dezimalzahlen (plus, da der Bildschirm des Rechners nur so groß ist, kann nicht die ganze Antwort angezeigt werden.) In diesem Fall möchten wir vielleicht unsere Antwort als einfach 1250 darstellen7 oder vereinfachen Sie die Antwort, indem Sie sie in wissenschaftlicher Notation schreiben.
-
 4 Versuchen Sie, Ihre Fähigkeiten zu erweitern. Wenn Sie mit der grundlegenden Algebra vertraut sind, versuchen Sie es mit Factoring. Eine der schwierigsten Algebra-Fähigkeiten von allen ist Factoring - eine Art Abkürzung, um komplexe Gleichungen in einfache Formen zu bringen. Factoring ist ein Semi-Advanced Algebra-Thema, also ziehen Sie in Betracht, den oben verlinkten Artikel zu Rate zu ziehen, wenn Sie Schwierigkeiten haben, ihn zu meistern. Im Folgenden finden Sie nur einige kurze Tipps zum Faktorisieren von Gleichungen:
4 Versuchen Sie, Ihre Fähigkeiten zu erweitern. Wenn Sie mit der grundlegenden Algebra vertraut sind, versuchen Sie es mit Factoring. Eine der schwierigsten Algebra-Fähigkeiten von allen ist Factoring - eine Art Abkürzung, um komplexe Gleichungen in einfache Formen zu bringen. Factoring ist ein Semi-Advanced Algebra-Thema, also ziehen Sie in Betracht, den oben verlinkten Artikel zu Rate zu ziehen, wenn Sie Schwierigkeiten haben, ihn zu meistern. Im Folgenden finden Sie nur einige kurze Tipps zum Faktorisieren von Gleichungen: - Gleichungen mit der Form ax + ba factor zu a (x + b). Beispiel: 2x + 4 = 2 (x + 2)
- Gleichungen mit der Form ax2 + bx Faktor zu cx ((a / c) x + (b / c)) wobei c die größte Zahl ist, die gleichmäßig in a und b unterteilt ist. Beispiel: 3Jahr2 + 12y = 3y (y + 4)
- Gleichungen mit der Form x2 + bx + c Faktor zu (x + y) (x + z) wobei y × z = c und yx + zx = bx. Beispiel: x2 + 4x + 3 = (x + 3) (x + 1).
-
 5 Üben, üben, üben! Fortschritte in der Algebra (und jede andere Art von Mathematik) erfordert viel harte Arbeit und Wiederholung. Machen Sie sich keine Sorgen - indem Sie im Unterricht aufpassen, all Ihre Aufgaben erledigen und Hilfe von Ihrem Lehrer oder anderen Schülern suchen, wenn Sie sie brauchen, wird Algebra zur zweiten Natur.
5 Üben, üben, üben! Fortschritte in der Algebra (und jede andere Art von Mathematik) erfordert viel harte Arbeit und Wiederholung. Machen Sie sich keine Sorgen - indem Sie im Unterricht aufpassen, all Ihre Aufgaben erledigen und Hilfe von Ihrem Lehrer oder anderen Schülern suchen, wenn Sie sie brauchen, wird Algebra zur zweiten Natur. -
 6 Bitten Sie Ihren Lehrer, Ihnen zu helfen, schwierige Algebra-Themen zu verstehen. Wenn es dir schwer fällt, Algebra in den Griff zu bekommen, mach dir keine Sorgen - du musst es nicht selbst lernen. Ihr Lehrer ist die erste Person, an die Sie sich mit Fragen wenden sollten. Fragen Sie nach dem Unterricht höflich Ihren Lehrer um Hilfe. Gute Lehrer werden in der Regel bereit sein, das Thema des Tages bei einem Termin nach der Schule neu zu erklären, und können sogar in der Lage sein, Ihnen zusätzliches Übungsmaterial zu geben.
6 Bitten Sie Ihren Lehrer, Ihnen zu helfen, schwierige Algebra-Themen zu verstehen. Wenn es dir schwer fällt, Algebra in den Griff zu bekommen, mach dir keine Sorgen - du musst es nicht selbst lernen. Ihr Lehrer ist die erste Person, an die Sie sich mit Fragen wenden sollten. Fragen Sie nach dem Unterricht höflich Ihren Lehrer um Hilfe. Gute Lehrer werden in der Regel bereit sein, das Thema des Tages bei einem Termin nach der Schule neu zu erklären, und können sogar in der Lage sein, Ihnen zusätzliches Übungsmaterial zu geben. - Wenn Ihr Lehrer Ihnen aus irgendeinem Grund nicht helfen kann, fragen Sie ihn nach Nachhilfemöglichkeiten in Ihrer Schule. Viele Schulen haben eine Art Nachschulprogramm, das Ihnen hilft, die zusätzliche Zeit und Aufmerksamkeit zu bekommen, die Sie benötigen, um mit Ihrer Algebra zu glänzen. Denken Sie daran, dass Ihnen die kostenlose Hilfe, die Ihnen zur Verfügung steht, nicht peinlich ist - es ist ein Zeichen dafür, dass Sie schlau genug sind, Ihr Problem zu lösen!
Teil fünf von fünf:
Erforschen von Zwischenthemen
-
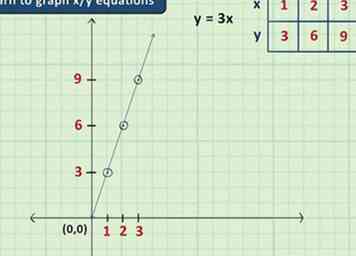 1 Lernen Sie, x / y-Gleichungen zu zeichnen. Diagramme können wertvolle Werkzeuge in der Algebra sein, da sie Ihnen ermöglichen, Ideen, für die Sie normalerweise Zahlen benötigen, in leicht verständlichen Bildern anzuzeigen. Üblicherweise sind Graphing-Probleme in der Anfangalgebra auf Gleichungen mit zwei Variablen (normalerweise x und y) beschränkt und werden in einem einfachen 2-D-Graphen mit einer x-Achse und einer y-Achse ausgeführt. Mit diesen Gleichungen müssen Sie nur einen Wert für x eingeben und dann nach y auflösen (oder umgekehrt), um zwei Zahlen zu erhalten, die einem Punkt im Diagramm entsprechen.
1 Lernen Sie, x / y-Gleichungen zu zeichnen. Diagramme können wertvolle Werkzeuge in der Algebra sein, da sie Ihnen ermöglichen, Ideen, für die Sie normalerweise Zahlen benötigen, in leicht verständlichen Bildern anzuzeigen. Üblicherweise sind Graphing-Probleme in der Anfangalgebra auf Gleichungen mit zwei Variablen (normalerweise x und y) beschränkt und werden in einem einfachen 2-D-Graphen mit einer x-Achse und einer y-Achse ausgeführt. Mit diesen Gleichungen müssen Sie nur einen Wert für x eingeben und dann nach y auflösen (oder umgekehrt), um zwei Zahlen zu erhalten, die einem Punkt im Diagramm entsprechen. - Wenn wir beispielsweise in der Gleichung y = 3x 2 für x einfügen, erhalten wir y = 6. Dies bedeutet, dass der Punkt (2,6) (zwei Räume rechts von der Mitte und sechs Räume über der Mitte) ist Teil der Grafik dieser Gleichung.
- Gleichungen mit der Form y = mx + b (wobei m und b Zahlen sind) sind insbesondere üblich in der Algebra. Diese Gleichungen haben immer eine Steigung von m und kreuzen die y-Achse bei y = b.
-
 2 Lerne Ungleichheiten zu lösen. Was machen Sie, wenn Ihre Gleichung kein Gleichheitszeichen verwendet? Nicht viel anders als das, was du normalerweise tun würdest, stellt sich heraus. Bei Ungleichungen, die Zeichen wie> ("größer als") und <("kleiner als") verwenden, lösen Sie einfach wie normal. Sie erhalten eine Antwort, die entweder kleiner oder größer als Ihre Variable ist.
2 Lerne Ungleichheiten zu lösen. Was machen Sie, wenn Ihre Gleichung kein Gleichheitszeichen verwendet? Nicht viel anders als das, was du normalerweise tun würdest, stellt sich heraus. Bei Ungleichungen, die Zeichen wie> ("größer als") und <("kleiner als") verwenden, lösen Sie einfach wie normal. Sie erhalten eine Antwort, die entweder kleiner oder größer als Ihre Variable ist. - Zum Beispiel würden wir mit der Gleichung 3> 5x - 2 genauso wie wir für eine normale Gleichung lösen:
-
- 3> 5x - 2
- 5> 5x
- 1> x, oder x <1.
-
- Das bedeutet, dass jede Zahl weniger als eins funktioniert für x. Mit anderen Worten, x kann 0, -1, -2 usw. sein. Wenn wir diese Zahlen in die Gleichung für x einschließen, erhalten wir immer eine Antwort kleiner als 3.
- Zum Beispiel würden wir mit der Gleichung 3> 5x - 2 genauso wie wir für eine normale Gleichung lösen:
-
 3 Tackle quadratische Gleichungen. Ein Algebra-Thema, mit dem viele Anfänger Schwierigkeiten haben, ist das Lösen von quadratischen Gleichungen. Quadrate sind Gleichungen mit der Form ax2 + bx + c = 0, wobei a, b und c Zahlen sind (außer dass a nicht 0 sein kann). Diese Gleichungen werden mit der Formel x = [-b +/- √ (b2 - 4ac)] / 2a. Seien Sie vorsichtig - das Vorzeichen bedeutet, dass Sie die Antworten zum Hinzufügen finden müssen und Subtrahieren, so können Sie zwei Antworten für diese Art von Problemen haben.
3 Tackle quadratische Gleichungen. Ein Algebra-Thema, mit dem viele Anfänger Schwierigkeiten haben, ist das Lösen von quadratischen Gleichungen. Quadrate sind Gleichungen mit der Form ax2 + bx + c = 0, wobei a, b und c Zahlen sind (außer dass a nicht 0 sein kann). Diese Gleichungen werden mit der Formel x = [-b +/- √ (b2 - 4ac)] / 2a. Seien Sie vorsichtig - das Vorzeichen bedeutet, dass Sie die Antworten zum Hinzufügen finden müssen und Subtrahieren, so können Sie zwei Antworten für diese Art von Problemen haben. - Lassen Sie uns als Beispiel die quadratische Formel 3x lösen2 + 2x -1 = 0.
-
- x = [-b +/- √ (b2 - 4ac)] / 2a
- x = [-2 +/- √ (22 - 4(3)(-1))]/2(3)
- x = [-2 +/- √ (4 - (-12))] / 6
- x = [-2 +/- √ (16)] / 6
- x = [-2 +/- 4] / 6
- x = -1 und 1/3
-
- Lassen Sie uns als Beispiel die quadratische Formel 3x lösen2 + 2x -1 = 0.
-
 4 Experimentieren Sie mit Gleichungssystemen. Mehr als eine Gleichung auf einmal zu lösen, klingt vielleicht super-tricky, aber wenn Sie mit einfachen Algebra-Gleichungen arbeiten, ist es nicht wirklich so schwer. Oft verwenden Algebra-Lehrer einen graphischen Ansatz, um diese Probleme zu lösen. Wenn Sie mit einem System aus zwei Gleichungen arbeiten, sind die Lösungen die Punkte in einem Diagramm, über die sich die Linien für beide Gleichungen kreuzen.
4 Experimentieren Sie mit Gleichungssystemen. Mehr als eine Gleichung auf einmal zu lösen, klingt vielleicht super-tricky, aber wenn Sie mit einfachen Algebra-Gleichungen arbeiten, ist es nicht wirklich so schwer. Oft verwenden Algebra-Lehrer einen graphischen Ansatz, um diese Probleme zu lösen. Wenn Sie mit einem System aus zwei Gleichungen arbeiten, sind die Lösungen die Punkte in einem Diagramm, über die sich die Linien für beide Gleichungen kreuzen. - Angenommen, wir arbeiten mit einem System, das die Gleichungen y = 3x - 2 und y = -x - 6 enthält. Wenn wir diese beiden Linien in einem Graphen zeichnen, erhalten wir eine Linie, die in einem steilen Winkel hochgeht und einer, der in einem milden Winkel untergeht. Da diese Linien sich am Punkt kreuzen (-1,-5)Dies ist eine Lösung für das System.[1]
- Wenn wir unser Problem überprüfen wollen, können wir dies tun, indem wir unsere Antwort in die Gleichungen des Systems einfügen - eine richtige Antwort sollte für beide "funktionieren".
-
- y = 3x - 2
- -5 = 3(-1) - 2
- -5 = -3 - 2
- -5 = -5
- y = -x - 6
- -5 = -(-1) - 6
- -5 = 1 - 6
- -5 = -5
-
- Beide Gleichungen "checken" aus, also ist unsere Antwort richtig!
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Überprüfen Sie Ihre grundlegenden mathematischen Operationen. Um Algebra zu lernen, müssen Sie grundlegende mathematische Fähigkeiten wie Addieren, Subtrahieren, Multiplizieren und Dividieren kennen. Diese Grund- / Grundschulmathematik ist wichtig, bevor Sie anfangen, Algebra zu lernen. Wenn Sie diese Fähigkeiten nicht beherrschen, wird es schwierig, die komplexeren Konzepte der Algebra zu bewältigen. Wenn Sie diese Operationen auffrischen möchten, lesen Sie unseren Artikel über grundlegende mathematische Fähigkeiten.
1 Überprüfen Sie Ihre grundlegenden mathematischen Operationen. Um Algebra zu lernen, müssen Sie grundlegende mathematische Fähigkeiten wie Addieren, Subtrahieren, Multiplizieren und Dividieren kennen. Diese Grund- / Grundschulmathematik ist wichtig, bevor Sie anfangen, Algebra zu lernen. Wenn Sie diese Fähigkeiten nicht beherrschen, wird es schwierig, die komplexeren Konzepte der Algebra zu bewältigen. Wenn Sie diese Operationen auffrischen möchten, lesen Sie unseren Artikel über grundlegende mathematische Fähigkeiten.  2 Kennen Sie die Reihenfolge der Vorgänge. Eines der schwierigsten Dinge beim Lösen einer Algebra-Gleichung als Anfänger ist zu wissen, wo ich anfangen soll. Glücklicherweise gibt es eine bestimmte Reihenfolge, um diese Probleme zu lösen: machen Sie zuerst alle mathematischen Operationen in Klammern, dann tun Sie Exponenten, dann multiplizieren Sie, dann teilen Sie, fügen Sie dann hinzu, und subtrahieren Sie schließlich. Ein praktisches Werkzeug zur Erinnerung an diese Reihenfolge von Operationen ist das Akronym PEMDAS. Hier erfahren Sie, wie Sie die Reihenfolge der Operationen anwenden. Zur Erinnerung, die Reihenfolge der Operationen ist:
2 Kennen Sie die Reihenfolge der Vorgänge. Eines der schwierigsten Dinge beim Lösen einer Algebra-Gleichung als Anfänger ist zu wissen, wo ich anfangen soll. Glücklicherweise gibt es eine bestimmte Reihenfolge, um diese Probleme zu lösen: machen Sie zuerst alle mathematischen Operationen in Klammern, dann tun Sie Exponenten, dann multiplizieren Sie, dann teilen Sie, fügen Sie dann hinzu, und subtrahieren Sie schließlich. Ein praktisches Werkzeug zur Erinnerung an diese Reihenfolge von Operationen ist das Akronym PEMDAS. Hier erfahren Sie, wie Sie die Reihenfolge der Operationen anwenden. Zur Erinnerung, die Reihenfolge der Operationen ist: 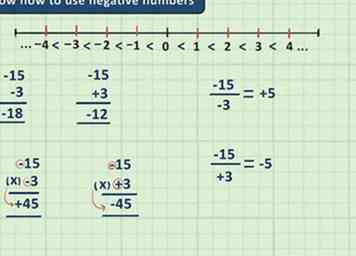 3 Wissen, wie man negative Zahlen benutzt. In der Algebra ist es üblich, negative Zahlen zu verwenden. Daher ist es ratsam zu überprüfen, wie man Negative addiert, subtrahiert, multipliziert und teilt, bevor man mit Algebra beginnt. Im Folgenden sind nur ein paar Zahlen zu negativen Zahlen zu beachten. Weitere Informationen finden Sie in unseren Artikeln zum Hinzufügen und Subtrahieren negativer Zahlen und zum Dividieren und Multiplizieren negativer Zahlen.
3 Wissen, wie man negative Zahlen benutzt. In der Algebra ist es üblich, negative Zahlen zu verwenden. Daher ist es ratsam zu überprüfen, wie man Negative addiert, subtrahiert, multipliziert und teilt, bevor man mit Algebra beginnt. Im Folgenden sind nur ein paar Zahlen zu negativen Zahlen zu beachten. Weitere Informationen finden Sie in unseren Artikeln zum Hinzufügen und Subtrahieren negativer Zahlen und zum Dividieren und Multiplizieren negativer Zahlen.  4 Wissen, wie man lange Probleme organisiert. Während einfache Algebra-Probleme ein Kinderspiel sein können, können kompliziertere Probleme viele, viele Schritte erfordern. Um Fehler zu vermeiden, sollten Sie Ihre Arbeit organisieren, indem Sie jedes Mal eine neue Zeile beginnen, wenn Sie einen Schritt zur Lösung Ihres Problems machen. Wenn Sie mit einer zweiseitigen Gleichung arbeiten, versuchen Sie, alle Gleichheitszeichen ("=" s) untereinander zu schreiben. Auf diese Weise, wenn Sie irgendwo einen Fehler machen, wird es viel einfacher zu finden und zu korrigieren.
4 Wissen, wie man lange Probleme organisiert. Während einfache Algebra-Probleme ein Kinderspiel sein können, können kompliziertere Probleme viele, viele Schritte erfordern. Um Fehler zu vermeiden, sollten Sie Ihre Arbeit organisieren, indem Sie jedes Mal eine neue Zeile beginnen, wenn Sie einen Schritt zur Lösung Ihres Problems machen. Wenn Sie mit einer zweiseitigen Gleichung arbeiten, versuchen Sie, alle Gleichheitszeichen ("=" s) untereinander zu schreiben. Auf diese Weise, wenn Sie irgendwo einen Fehler machen, wird es viel einfacher zu finden und zu korrigieren.  1 Suchen Sie nach Symbolen, die keine Zahlen sind. In der Algebra werden Sie anfangen, Buchstaben und Symbole in Ihren mathematischen Problemen zu sehen, und nicht nur Zahlen. Dies nennt man Variablen. Variablen sind nicht so verwirrend, wie sie zuerst erscheinen - sie sind nur Möglichkeiten, Zahlen mit unbekannten Werten zu zeigen. Im Folgenden finden Sie nur einige häufige Beispiele für Variablen in der Algebra:
1 Suchen Sie nach Symbolen, die keine Zahlen sind. In der Algebra werden Sie anfangen, Buchstaben und Symbole in Ihren mathematischen Problemen zu sehen, und nicht nur Zahlen. Dies nennt man Variablen. Variablen sind nicht so verwirrend, wie sie zuerst erscheinen - sie sind nur Möglichkeiten, Zahlen mit unbekannten Werten zu zeigen. Im Folgenden finden Sie nur einige häufige Beispiele für Variablen in der Algebra:  2 Stellen Sie sich Variablen als "unbekannte" Zahlen vor. Wie oben erwähnt, sind Variablen im Grunde nur Zahlen mit unbekannten Werten. Mit anderen Worten, da ist eine Nummer das kann anstelle der Variablen gehen, damit die Gleichung funktioniert. Normalerweise ist Ihr Ziel in einem Algebra-Problem, herauszufinden, was die Variable ist - denken Sie an sie als eine "Mystery-Nummer", die Sie zu entdecken versuchen.
2 Stellen Sie sich Variablen als "unbekannte" Zahlen vor. Wie oben erwähnt, sind Variablen im Grunde nur Zahlen mit unbekannten Werten. Mit anderen Worten, da ist eine Nummer das kann anstelle der Variablen gehen, damit die Gleichung funktioniert. Normalerweise ist Ihr Ziel in einem Algebra-Problem, herauszufinden, was die Variable ist - denken Sie an sie als eine "Mystery-Nummer", die Sie zu entdecken versuchen.  3 Achten Sie auf wiederkehrende Variablen. Wenn eine Variable mehr als einmal auftritt, vereinfachen Sie die Variablen. Was tun Sie, wenn die gleiche Variable mehr als einmal in der Gleichung erscheint? Obwohl diese Situation schwierig zu lösen scheint, können Sie Variablen tatsächlich behandeln, wie Sie normale Zahlen behandeln würden - mit anderen Worten, Sie können sie hinzufügen, subtrahieren und so weiter, solange Sie nur identische Variablen kombinieren. Mit anderen Worten, x + x = 2x, aber x + y ist nicht gleich 2xy.
3 Achten Sie auf wiederkehrende Variablen. Wenn eine Variable mehr als einmal auftritt, vereinfachen Sie die Variablen. Was tun Sie, wenn die gleiche Variable mehr als einmal in der Gleichung erscheint? Obwohl diese Situation schwierig zu lösen scheint, können Sie Variablen tatsächlich behandeln, wie Sie normale Zahlen behandeln würden - mit anderen Worten, Sie können sie hinzufügen, subtrahieren und so weiter, solange Sie nur identische Variablen kombinieren. Mit anderen Worten, x + x = 2x, aber x + y ist nicht gleich 2xy.  1 Versuchen Sie, die Variable selbst in Algebra-Gleichungen zu erhalten. Das Lösen einer Gleichung in der Algebra bedeutet normalerweise, herauszufinden, was die Variable ist. Algebra-Gleichungen werden normalerweise mit Zahlen und / oder Variablen auf beiden Seiten erstellt, wie folgt: x + 2 = 9 × 4. Um herauszufinden, was die Variable ist, müssen Sie sie selbst auf einer Seite des Gleichheitszeichens erhalten. Was immer auf der anderen Seite des Gleichheitszeichens ist, ist deine Antwort.
1 Versuchen Sie, die Variable selbst in Algebra-Gleichungen zu erhalten. Das Lösen einer Gleichung in der Algebra bedeutet normalerweise, herauszufinden, was die Variable ist. Algebra-Gleichungen werden normalerweise mit Zahlen und / oder Variablen auf beiden Seiten erstellt, wie folgt: x + 2 = 9 × 4. Um herauszufinden, was die Variable ist, müssen Sie sie selbst auf einer Seite des Gleichheitszeichens erhalten. Was immer auf der anderen Seite des Gleichheitszeichens ist, ist deine Antwort.  2 Addition mit Subtraktion abbrechen (und umgekehrt). Wie wir gerade oben gesehen haben, bedeutet es, wenn man x auf einer Seite des Gleichheitszeichens erhält, normalerweise die Zahlen daneben loszuwerden. Um dies zu tun, führen wir die "entgegengesetzte" Operation auf beiden Seiten der Gleichung durch. Zum Beispiel, in der Gleichung x + 3 = 0, da wir ein "+ 3" neben unserem x sehen, setzen wir eine "- 3" auf beide Seiten. Die "+ 3" und "- 3", x auf sich selbst und "-3" auf der anderen Seite des Gleichheitszeichens, wie folgt: x = -3.
2 Addition mit Subtraktion abbrechen (und umgekehrt). Wie wir gerade oben gesehen haben, bedeutet es, wenn man x auf einer Seite des Gleichheitszeichens erhält, normalerweise die Zahlen daneben loszuwerden. Um dies zu tun, führen wir die "entgegengesetzte" Operation auf beiden Seiten der Gleichung durch. Zum Beispiel, in der Gleichung x + 3 = 0, da wir ein "+ 3" neben unserem x sehen, setzen wir eine "- 3" auf beide Seiten. Die "+ 3" und "- 3", x auf sich selbst und "-3" auf der anderen Seite des Gleichheitszeichens, wie folgt: x = -3.  3 Multiplikation mit Division abbrechen (und umgekehrt). Multiplikation und Division sind etwas schwieriger zu bearbeiten als Addition und Subtraktion, aber sie haben die gleiche "umgekehrte" Beziehung. Wenn Sie auf einer Seite ein "× 3" sehen, werden Sie es abbrechen, indem Sie beide Seiten durch 3 teilen, und so weiter.
3 Multiplikation mit Division abbrechen (und umgekehrt). Multiplikation und Division sind etwas schwieriger zu bearbeiten als Addition und Subtraktion, aber sie haben die gleiche "umgekehrte" Beziehung. Wenn Sie auf einer Seite ein "× 3" sehen, werden Sie es abbrechen, indem Sie beide Seiten durch 3 teilen, und so weiter.  4 Brechen Sie Exponenten ab, indem Sie die Wurzel nehmen (und umgekehrt). Exponenten sind ein ziemlich fortgeschrittenes Voralgebra-Thema - wenn Sie nicht wissen, wie Sie es tun, finden Sie in unserem grundlegenden Exponenten Artikel für weitere Informationen. Das "Gegenteil" eines Exponenten ist die Wurzel, die dieselbe Zahl hat wie sie. Zum Beispiel das Gegenteil von der 2 Exponent ist eine Quadratwurzel (√), das Gegenteil von der 3 Exponent ist die Kubikwurzel (3√) und so weiter.
4 Brechen Sie Exponenten ab, indem Sie die Wurzel nehmen (und umgekehrt). Exponenten sind ein ziemlich fortgeschrittenes Voralgebra-Thema - wenn Sie nicht wissen, wie Sie es tun, finden Sie in unserem grundlegenden Exponenten Artikel für weitere Informationen. Das "Gegenteil" eines Exponenten ist die Wurzel, die dieselbe Zahl hat wie sie. Zum Beispiel das Gegenteil von der 2 Exponent ist eine Quadratwurzel (√), das Gegenteil von der 3 Exponent ist die Kubikwurzel (3√) und so weiter.  1 Verwenden Sie Bilder, um Probleme zu verdeutlichen. Wenn Sie Probleme bei der Visualisierung eines Algebraproblems haben, versuchen Sie es mit Hilfe von Diagrammen oder Bildern, um Ihre Gleichung zu veranschaulichen. Sie können sogar versuchen, eine Gruppe von physischen Objekten (wie Blöcke oder Münzen) zu verwenden, wenn Sie etwas handliches haben.
1 Verwenden Sie Bilder, um Probleme zu verdeutlichen. Wenn Sie Probleme bei der Visualisierung eines Algebraproblems haben, versuchen Sie es mit Hilfe von Diagrammen oder Bildern, um Ihre Gleichung zu veranschaulichen. Sie können sogar versuchen, eine Gruppe von physischen Objekten (wie Blöcke oder Münzen) zu verwenden, wenn Sie etwas handliches haben.  2 Verwenden Sie "Common-Sense-Checks" (besonders bei Wortproblemen). Versuchen Sie beim Konvertieren eines Wortproblems in Algebra Ihre Formel zu überprüfen, indem Sie einfache Werte für Ihre Variable einfügen. Ist Ihre Gleichung sinnvoll, wenn x = 0? Wenn x = 1? Wenn x = -1? Es ist leicht, einfache Fehler zu machen, indem du p = 6d aufschreibst, wenn du p = d / 6 meinst, aber diese werden leicht aufgefangen, wenn du eine schnelle Vernunftprüfung an deiner Arbeit durchführst, bevor du weiter gehst.
2 Verwenden Sie "Common-Sense-Checks" (besonders bei Wortproblemen). Versuchen Sie beim Konvertieren eines Wortproblems in Algebra Ihre Formel zu überprüfen, indem Sie einfache Werte für Ihre Variable einfügen. Ist Ihre Gleichung sinnvoll, wenn x = 0? Wenn x = 1? Wenn x = -1? Es ist leicht, einfache Fehler zu machen, indem du p = 6d aufschreibst, wenn du p = d / 6 meinst, aber diese werden leicht aufgefangen, wenn du eine schnelle Vernunftprüfung an deiner Arbeit durchführst, bevor du weiter gehst.  3 Seien Sie sich bewusst, dass die Antworten in der Algebra nicht immer ganzzahlig sind. Die Antworten auf Algebra und andere fortgeschrittene Formen der Mathematik sind nicht immer runde, einfache Zahlen. Sie können oft Dezimalzahlen, Brüche oder irrationale Zahlen sein. Ein Taschenrechner kann Ihnen helfen, diese komplizierten Antworten zu finden, aber denken Sie daran, dass Ihr Lehrer möglicherweise verlangt, dass Sie Ihre Antwort in ihrer genauen Form und nicht in einer unhandlichen Dezimalzahl geben.
3 Seien Sie sich bewusst, dass die Antworten in der Algebra nicht immer ganzzahlig sind. Die Antworten auf Algebra und andere fortgeschrittene Formen der Mathematik sind nicht immer runde, einfache Zahlen. Sie können oft Dezimalzahlen, Brüche oder irrationale Zahlen sein. Ein Taschenrechner kann Ihnen helfen, diese komplizierten Antworten zu finden, aber denken Sie daran, dass Ihr Lehrer möglicherweise verlangt, dass Sie Ihre Antwort in ihrer genauen Form und nicht in einer unhandlichen Dezimalzahl geben.  4 Versuchen Sie, Ihre Fähigkeiten zu erweitern. Wenn Sie mit der grundlegenden Algebra vertraut sind, versuchen Sie es mit Factoring. Eine der schwierigsten Algebra-Fähigkeiten von allen ist Factoring - eine Art Abkürzung, um komplexe Gleichungen in einfache Formen zu bringen. Factoring ist ein Semi-Advanced Algebra-Thema, also ziehen Sie in Betracht, den oben verlinkten Artikel zu Rate zu ziehen, wenn Sie Schwierigkeiten haben, ihn zu meistern. Im Folgenden finden Sie nur einige kurze Tipps zum Faktorisieren von Gleichungen:
4 Versuchen Sie, Ihre Fähigkeiten zu erweitern. Wenn Sie mit der grundlegenden Algebra vertraut sind, versuchen Sie es mit Factoring. Eine der schwierigsten Algebra-Fähigkeiten von allen ist Factoring - eine Art Abkürzung, um komplexe Gleichungen in einfache Formen zu bringen. Factoring ist ein Semi-Advanced Algebra-Thema, also ziehen Sie in Betracht, den oben verlinkten Artikel zu Rate zu ziehen, wenn Sie Schwierigkeiten haben, ihn zu meistern. Im Folgenden finden Sie nur einige kurze Tipps zum Faktorisieren von Gleichungen:  5 Üben, üben, üben! Fortschritte in der Algebra (und jede andere Art von Mathematik) erfordert viel harte Arbeit und Wiederholung. Machen Sie sich keine Sorgen - indem Sie im Unterricht aufpassen, all Ihre Aufgaben erledigen und Hilfe von Ihrem Lehrer oder anderen Schülern suchen, wenn Sie sie brauchen, wird Algebra zur zweiten Natur.
5 Üben, üben, üben! Fortschritte in der Algebra (und jede andere Art von Mathematik) erfordert viel harte Arbeit und Wiederholung. Machen Sie sich keine Sorgen - indem Sie im Unterricht aufpassen, all Ihre Aufgaben erledigen und Hilfe von Ihrem Lehrer oder anderen Schülern suchen, wenn Sie sie brauchen, wird Algebra zur zweiten Natur.  6 Bitten Sie Ihren Lehrer, Ihnen zu helfen, schwierige Algebra-Themen zu verstehen. Wenn es dir schwer fällt, Algebra in den Griff zu bekommen, mach dir keine Sorgen - du musst es nicht selbst lernen. Ihr Lehrer ist die erste Person, an die Sie sich mit Fragen wenden sollten. Fragen Sie nach dem Unterricht höflich Ihren Lehrer um Hilfe. Gute Lehrer werden in der Regel bereit sein, das Thema des Tages bei einem Termin nach der Schule neu zu erklären, und können sogar in der Lage sein, Ihnen zusätzliches Übungsmaterial zu geben.
6 Bitten Sie Ihren Lehrer, Ihnen zu helfen, schwierige Algebra-Themen zu verstehen. Wenn es dir schwer fällt, Algebra in den Griff zu bekommen, mach dir keine Sorgen - du musst es nicht selbst lernen. Ihr Lehrer ist die erste Person, an die Sie sich mit Fragen wenden sollten. Fragen Sie nach dem Unterricht höflich Ihren Lehrer um Hilfe. Gute Lehrer werden in der Regel bereit sein, das Thema des Tages bei einem Termin nach der Schule neu zu erklären, und können sogar in der Lage sein, Ihnen zusätzliches Übungsmaterial zu geben.  1 Lernen Sie, x / y-Gleichungen zu zeichnen. Diagramme können wertvolle Werkzeuge in der Algebra sein, da sie Ihnen ermöglichen, Ideen, für die Sie normalerweise Zahlen benötigen, in leicht verständlichen Bildern anzuzeigen. Üblicherweise sind Graphing-Probleme in der Anfangalgebra auf Gleichungen mit zwei Variablen (normalerweise x und y) beschränkt und werden in einem einfachen 2-D-Graphen mit einer x-Achse und einer y-Achse ausgeführt. Mit diesen Gleichungen müssen Sie nur einen Wert für x eingeben und dann nach y auflösen (oder umgekehrt), um zwei Zahlen zu erhalten, die einem Punkt im Diagramm entsprechen.
1 Lernen Sie, x / y-Gleichungen zu zeichnen. Diagramme können wertvolle Werkzeuge in der Algebra sein, da sie Ihnen ermöglichen, Ideen, für die Sie normalerweise Zahlen benötigen, in leicht verständlichen Bildern anzuzeigen. Üblicherweise sind Graphing-Probleme in der Anfangalgebra auf Gleichungen mit zwei Variablen (normalerweise x und y) beschränkt und werden in einem einfachen 2-D-Graphen mit einer x-Achse und einer y-Achse ausgeführt. Mit diesen Gleichungen müssen Sie nur einen Wert für x eingeben und dann nach y auflösen (oder umgekehrt), um zwei Zahlen zu erhalten, die einem Punkt im Diagramm entsprechen.  2 Lerne Ungleichheiten zu lösen. Was machen Sie, wenn Ihre Gleichung kein Gleichheitszeichen verwendet? Nicht viel anders als das, was du normalerweise tun würdest, stellt sich heraus. Bei Ungleichungen, die Zeichen wie> ("größer als") und <("kleiner als") verwenden, lösen Sie einfach wie normal. Sie erhalten eine Antwort, die entweder kleiner oder größer als Ihre Variable ist.
2 Lerne Ungleichheiten zu lösen. Was machen Sie, wenn Ihre Gleichung kein Gleichheitszeichen verwendet? Nicht viel anders als das, was du normalerweise tun würdest, stellt sich heraus. Bei Ungleichungen, die Zeichen wie> ("größer als") und <("kleiner als") verwenden, lösen Sie einfach wie normal. Sie erhalten eine Antwort, die entweder kleiner oder größer als Ihre Variable ist.  3 Tackle quadratische Gleichungen. Ein Algebra-Thema, mit dem viele Anfänger Schwierigkeiten haben, ist das Lösen von quadratischen Gleichungen. Quadrate sind Gleichungen mit der Form ax2 + bx + c = 0, wobei a, b und c Zahlen sind (außer dass a nicht 0 sein kann). Diese Gleichungen werden mit der Formel x = [-b +/- √ (b2 - 4ac)] / 2a. Seien Sie vorsichtig - das Vorzeichen bedeutet, dass Sie die Antworten zum Hinzufügen finden müssen und Subtrahieren, so können Sie zwei Antworten für diese Art von Problemen haben.
3 Tackle quadratische Gleichungen. Ein Algebra-Thema, mit dem viele Anfänger Schwierigkeiten haben, ist das Lösen von quadratischen Gleichungen. Quadrate sind Gleichungen mit der Form ax2 + bx + c = 0, wobei a, b und c Zahlen sind (außer dass a nicht 0 sein kann). Diese Gleichungen werden mit der Formel x = [-b +/- √ (b2 - 4ac)] / 2a. Seien Sie vorsichtig - das Vorzeichen bedeutet, dass Sie die Antworten zum Hinzufügen finden müssen und Subtrahieren, so können Sie zwei Antworten für diese Art von Problemen haben.  4 Experimentieren Sie mit Gleichungssystemen. Mehr als eine Gleichung auf einmal zu lösen, klingt vielleicht super-tricky, aber wenn Sie mit einfachen Algebra-Gleichungen arbeiten, ist es nicht wirklich so schwer. Oft verwenden Algebra-Lehrer einen graphischen Ansatz, um diese Probleme zu lösen. Wenn Sie mit einem System aus zwei Gleichungen arbeiten, sind die Lösungen die Punkte in einem Diagramm, über die sich die Linien für beide Gleichungen kreuzen.
4 Experimentieren Sie mit Gleichungssystemen. Mehr als eine Gleichung auf einmal zu lösen, klingt vielleicht super-tricky, aber wenn Sie mit einfachen Algebra-Gleichungen arbeiten, ist es nicht wirklich so schwer. Oft verwenden Algebra-Lehrer einen graphischen Ansatz, um diese Probleme zu lösen. Wenn Sie mit einem System aus zwei Gleichungen arbeiten, sind die Lösungen die Punkte in einem Diagramm, über die sich die Linien für beide Gleichungen kreuzen.